2023年10月16日
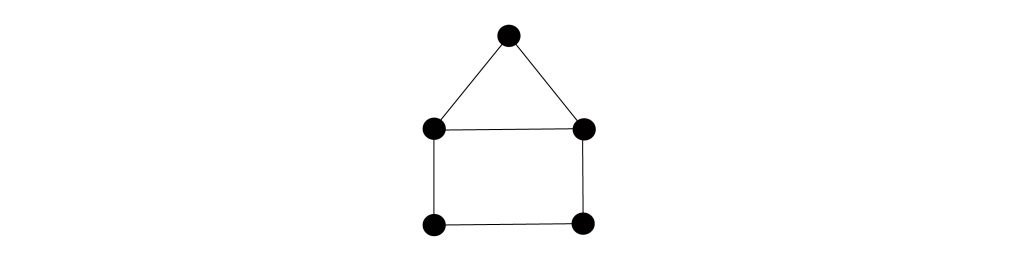
你有尝试过下图的脑力题吗?连点成线,组成房子的形状,必须一笔画完,不能回头。又或者,你点开过Facebook的好友推荐、玩过桌游“卡坦岛”吗?
(“画房子”智力题:连点成线,组成房子的形状,必须一笔画完,不能回头)
如果你有过上述任意经历,你就已经体会过了“图论”的一种形式。这一数学的分支深深吸引着西交利物浦大学数学物理学院大学数学系的刘旭钧博士。
“一开始我想研究的是其他数学领域,但却为图论证明的优雅所着迷。”刘旭钧博士说。
从A到B
图论是数学的一个分支,探索图的关系和特性——但这里指的并不是饼图和散点图。
那“图”到底是什么呢?
假如你想找到从伦敦坐火车去维也纳最高效的路线,你可以用点(数学中称为“顶点”)表示每个城市,用直线或者曲线表示城市之间的线路(称为“边”)。顶点和边组合起来就构成了图。
然后,就可以利用这个图来研究两个城市之间的换乘和路线。
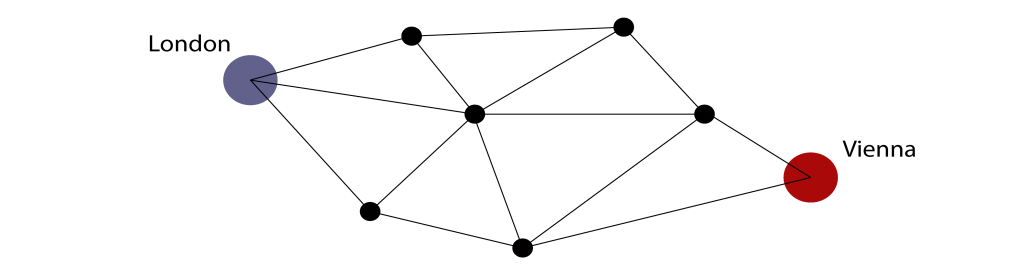
(乘火车从伦敦到维也纳:以“图”的形式展示途径小城市的可能路线)
通过图论,数学家可以对包括计算机科学、电气工程等各个领域的复杂网络进行建模和分析。
刘旭钧博士最近和美国大峡谷州立大学(Grand Valley State University)的Michael Santana和Taylor Short博士合作,解决了一个引起图论研究学者广泛关注的问题。
两点相邻,色不相同
团队研究针对一种图论理论——染色着色的主要目的是对图的某些部分进行标记,以符合某些规则,并避免特定的冲突。
试举一例:给下图的每个点着色,使得相邻两个点的颜色不相同。
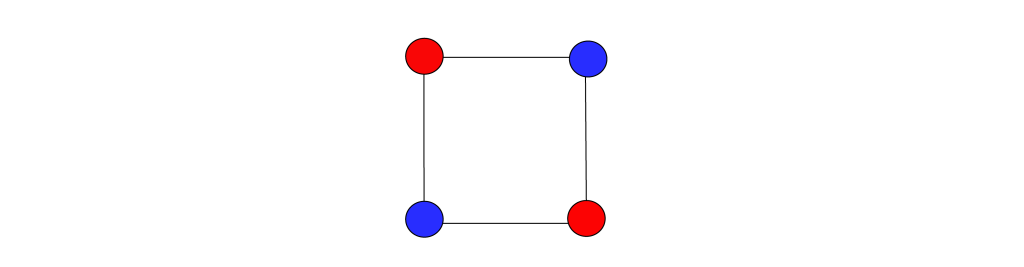
(“染色”示例:要想使四个点中相邻两点的颜色都不相同,至少需要两种颜色)
刘旭钧博士解释说:“我研究的着色叫做‘填装染色’,是由无线电网络中的频率分配问题所启发的。”
“世界各地有许多广播电台,我们要为每个电台分配一个频率;分配相同频率的电台必须至少相隔一定的距离,且每个频率需要不同的最小距离。”
“这就引发了一个问题——这样分配最少需要多少种频率?”
重要成果
在最新的研究中,刘旭钧博士和合作伙伴成功解决了数学家Hocquard、Lajou和Lužar于2022年在《图论杂志》中提出的问题。
该问题有关亚三正则图的分割,图中每个顶点(点)都有最多三条边(线)与之相连。
题目要求研究人员在已知有两种不同的边集的情况下,确定如何将边分割成多个部分。
- 第一种:要求每对边不共享端点(每条边有两个端点)。
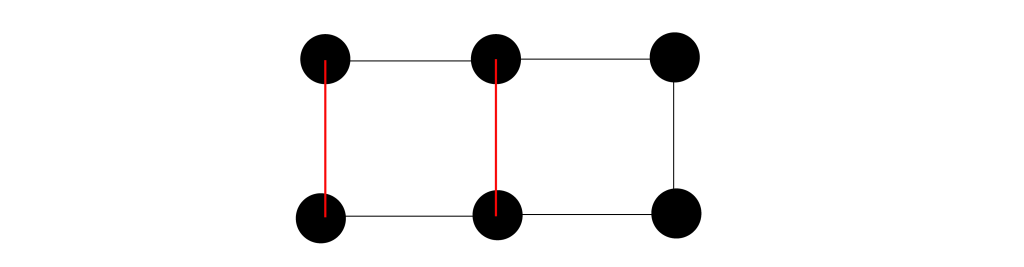
(例:不共享端点的一对边)
- 第二种:要求每对边不仅不共享端点,其端点还不由另一条边相连。
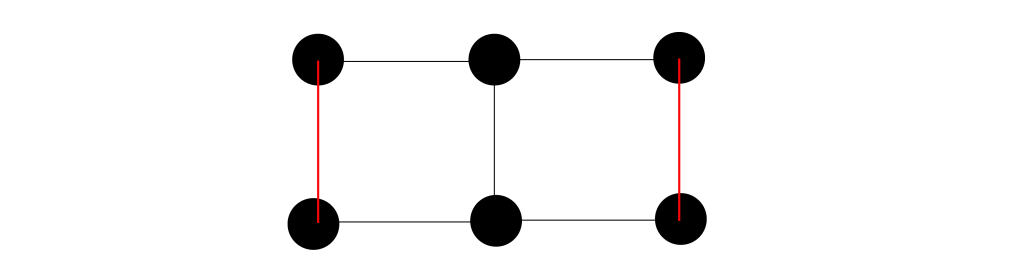
(例:两条边不共享端点,且端点不由另一条边相连)
团队着手解决的问题是:是否能在将第一种边集的数量固定为1的情况下,尽可能减少第二种边集的数量。
刘旭钧博士说:“通过解决这一猜想,我们也推动了对亚三正则图结构的理解,还有可能为解决著名的Erdős- Nešetřil猜想提供思路。研究成果也有助于解决通讯网络中的一些问题。”
自刘旭钧博士开始在伊利诺伊大学Alexandr Kostochka教授门下开展图论相关的博士研究以来,他与合作者们已经成功解决了多个猜想,包括2012年阿贝尔奖得主Szemerédi及其合作学者们共同提出的问题。
刘旭钧博士表示,自己将继续在该领域钻研更多问题。“我计划继续研究图的染色问题,研究重点是通过组合零点定理和基于概率方法等其他方法探索填装染色问题。”
他说:“我希望通过这些研究,对图论领域做出有意义的贡献。”
论文《每个亚三正则图都存在(1,2^7)-填装边染色》(Every subcubic multigraph is (1,2^7)-packing edge-colorable)发表于《图论杂志》。
刘旭钧博士还应邀在众多国内外学术会议上讲解该论文,包括第十届全国组合学与图论大会和中国运筹学会图论组合分会2023年年会等。

(刘旭钧博士在中国运筹学会图论组合分会2023年年会上发表演讲)
(记者:刘沁茹 Catherine Diamond 翻译:韩香音 编辑:石露芸)
2023年10月16日