实验原理
迈克尔逊实验仪 的光路如图所示:
实验中使用两个相干的单色点光源所产生的干涉称为非定域干涉。它的光程差可以用下式来描述:
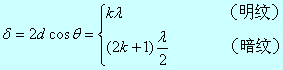
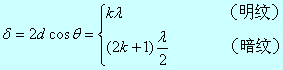
式中k为干涉条纹的级次,λ为光的波长。
由激光源产生的非定域干涉有如下特点:
(1)d、λ一定时,若θ= 0,光程差δ= 2d最大,即圆心所对应的干涉级次最高,从圆心向外的干涉级次依次降低。
(2)k、λ一定时,若d增大,θ随之增大,则条纹的半径也增大。可以看到,当d增大时,圆环一个个从中心“吐出”后向外扩张,干涉圆环的间隔变小,看上去条纹变细变密;当d减小时,圆环逐渐缩小,最后“吞进”在 中心处,干涉条纹变粗变疏。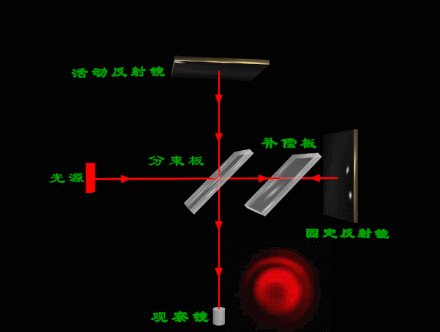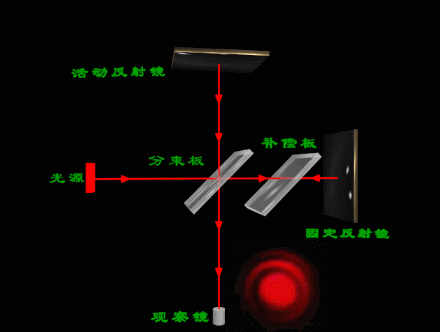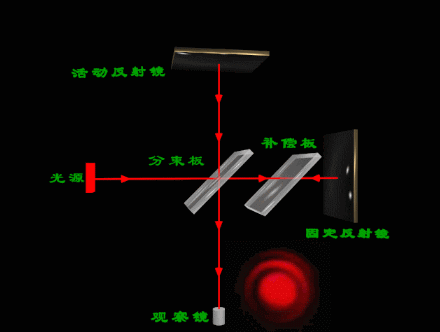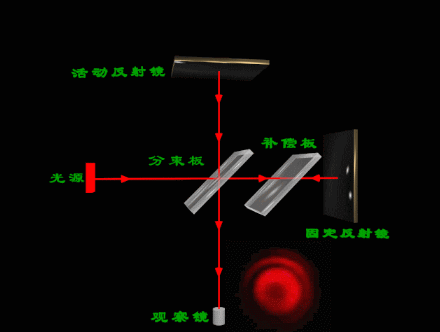
(3)对θ= 0的明条纹,有:δ=2d=kλ可见每“吐出”或“吞进”
一个圆环,相当于S1S2的光程差改变了一个波长Δδ=λ。
当d变化了Δd时,相应地“吐出”(或 “吞进”)的环数为Δk,则
![]()
从迈克尔逊干涉仪的读数系统上测出M1移动的距离Δd并数出相应的“吞
吐”环数Δk,就可以求出光的波长λ。
用迈克尔逊干涉仪还可以观测扩展的面光源产生的定域干涉条纹。定域干涉条纹的形状和定域的位置取决于M1、M2′的位置和取向,可分为等倾干涉和等厚干涉。
(1) 等倾干涉
图中两光束的光程差为:
![]()
![]()
当M1和M2′的间距d一定时,光程差只决定于入射角(出射角)θ。干涉条纹是一系列与不同倾角θ相对应的明暗相间的同心圆环形干涉条纹,称为等倾干涉条纹,与点光源产生的非定域干涉条纹类似。
(2)等厚干涉
当M1、M2′有一个很小的角度时,M1和M2′之间形成楔形空气薄层,就会出现等厚干涉条纹。
当M1和M2′之间的夹角很小时,光线“1”和“2”的光程差仍然可以近似地用式δ![]() 表示,其中d是观察点处空气层的厚度,θ仍为入射角。
表示,其中d是观察点处空气层的厚度,θ仍为入射角。
当入射角θ不大时,cosθ≈1,光程差δ =2d 光程差δ的变化主要决定于厚度d的变化。在楔形上厚度相同的地方光程差相同,因而这种干涉条纹称为等厚干涉条纹。
