发布时间:2024-02-24点击次数:
论文解读:丁建辉,李明哲,赵艳蓉,孙楚天
编者按
本次解读的文章发表于CCF-B类会议30th ACM International Conference on Information and Knowledge Management。摘要总结如下:
3维装箱问题(3D-BPP)不仅是组合优化的基础,而且在现实物流中也得到广泛应用。现代物流行业中,约束条件的复杂性、货物的异质性和订单规模急剧增加,给设计符合标准的包装方案带来了巨大的挑战。虽然树搜索算法被证明是解决3D-BPP 的成功范例,但在上述大规模场景中应用过于耗时。为了克服这个限制,论文提出了一种数据驱动的树搜索算法(DDTS)来解决3D-BPP问题。通过树搜索算法探索具有复杂约束的解空间,并用历史数据训练的卷积神经网络指导剪枝加速过程。真实数据集的计算实验表明,该算法优于最先进的方法,加载率提高了2.47%。此外,深度学习技术在性能损失0.04%的情况下,将搜索效率提高了37.14%。该算法已部署在华为物流系统中,装载率提高3%,每年可降低数百万美元的物流成本。据我们所知,本文是首次提出针对大规模 3D-BPP 进行深度剪枝网络树搜索。
1 问题背景
3D-BPP(三维装箱)问题不仅仅是组合优化问题的基础,更广泛应用在现实世界的物流体系中。但随着现实物流的发展需要,3D-BPP问题的约束越来越复杂、货物的异构性越来越强、订单规模越来越大,导致先前尚可维持运行的3D-BPP方案效率降低,难以满足现代物流的装箱需求,该研究致力于在前人研究的基础上提升算法效率,帮助降低物流成本。
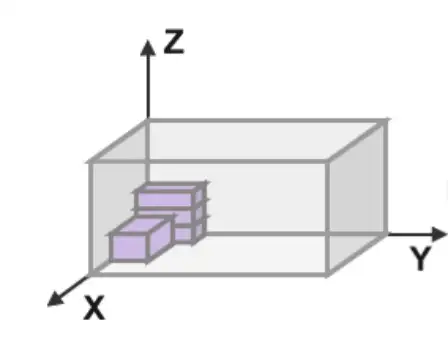
简单介绍下经典的3D-BPP问题:假设有n个长方体物品以及不定数量的长方体容器,它们均具有长、宽、高的属性,物品不允许旋转(即物品的长宽高不可以互换,只能保持与容器边缘平行的状态下放入),如图1所示。经典3D-BPP要解决的问题就是考虑如何合理地将物品摆放到容器中且所需容器数量最小。其常见相关要素可简单表示如下:
• 优化目标:最大化装载率、最小化装载容器(例如纸箱)的表面积等;
• 决策变量:物体放置顺序、物体放置的具体位置等;
• 约束:体积、重量、稳定性、重不压轻、物品价值最大化等;
此前有研究者用树搜索算法(Tree Search algorithm,TS)对此问题进行求解,但随着物流规模的增大,约束复杂度增加,TS类算法耗时逐渐增长。为了克服这个限制,这篇文章的研究人员提出了一种基于数据驱动的树搜索算法(Data-Driven Tree Search algorithm,DDTS),其作用原理是通过树搜索算法探索具有复杂约束的解空间,并且使用基于历史数据训练的卷积神经网络进行搜索剪枝以加速搜索的过程。
2 问题建模
任务类型:待装物体全部已知的离线装箱问题;
优化目标:假设给定容器T以及N个待装物体Item = {1...,i,...,N}。其中,容器T的规模为L(长),W(宽),H(高),第i个item的规模为Li,Wi,Hi。此外,引入变量qi表示item_i是否放置在当前的容器中。为了降低包装成本,即尽可能用较少的容器装下所有的物体,本文设计了如下的最大化容器装载率的目标:
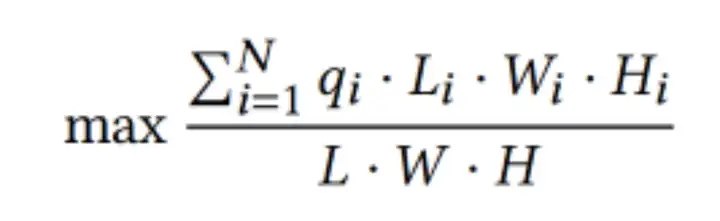
决策变量:从多个维度刻画,主要包括了物体的放置顺序及位置(x, y, z)等; 约束:总共包含了30+个约束,具体如下:
容器相关: a.形状约束:容器必须是规整的长方体; b.重量/体积限制:放在容器中的物体的总体积以及总体重不能超过容器的上限;
物体相关: a.形状约束:形状需要跟容器一样,必须是长方体; b.平行放置约束:物体的各个面必须跟容器的面并行,不能倾斜着放; c.后进先出约束:在卸货时,需要按照“后进先出”策略; d.方向约束:每个物体都有严格的可放置方向限制; e.易碎品约束:非易碎品不能放置在易碎品上面; f.支撑面约束:放置物体时,其底部的支撑区域占底面积的比例需要超过某个阈值;长度过高的物体上面只能放置1个物体;部分物体只能放在容器的底部; g.承载约束:物体的承载量不能超过它的上限等; h.高度约束:完成放置后,物体的总高度不能超过容器的高度; i.包装材料约束:编织袋不能放在纸箱上;
3 解决方案
这篇文章提出的方案主要包含3个模块:
块组装(Block building):将不同的items组合成blocks,核心作用是降低问题规模;
候选空间构建(Space generating):使用特定的策略划分空间,核心作用是构建可放置物体的候选空间;
树搜索算法(Tree search algrithm,核心贡献):使用结合机器学习的树搜索算法进行剪枝加速;
3.1 块组装 Block building
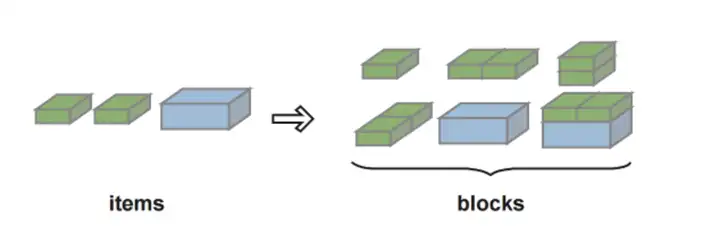
如图3所示,Block building的核心思想是利用特定的策略将不同item组装起来(item的规模可能是一样,也可能是不一样),从而形成多个block(本质是规模比较大的item)。形成block后,最大的好处是减少了需要放置的item的数量,继而降低了问题的求解复杂度,从而起到问题求解加速的效果。这种策略简单高效,在实际的离线装箱任务中经常使用。但是,通过深入分析可知,这种策略有1个比较明显的缺点,即组装过程跟装箱过程是解耦的,比较容易陷入局部较优解。
图4是本文使用的Block Building的伪代码,输入总共包含2项内容,待放置的item集合I以及它们的可放置方向O,经过一系列的遍历&判断逻辑,最终能获得对应的Block集合B。

3.2 候选空间构建 Space generating
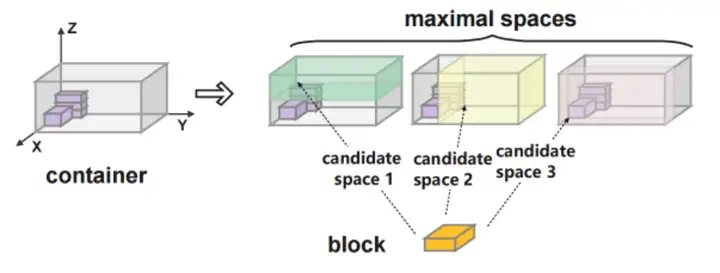
如图5所示,Space generating的核心思想是将当前的item放置好后,利用策略将剩余空间切分成多个可放置空间(通常每次切分,会新构建3个候选空间,这些空间可能会和过往的空间有重叠)。按照我的理解,这种做法本质也起到了降维的作用。原因在于有了这些空间后,可以直接将物体放到可放置候选空间的左下角,而不是漫无目的的将item放到可放置区域的任何位置。这2种做法的差异在于,前者形成的可候选位置是有限的,而后者是无限的,难度会大很多。
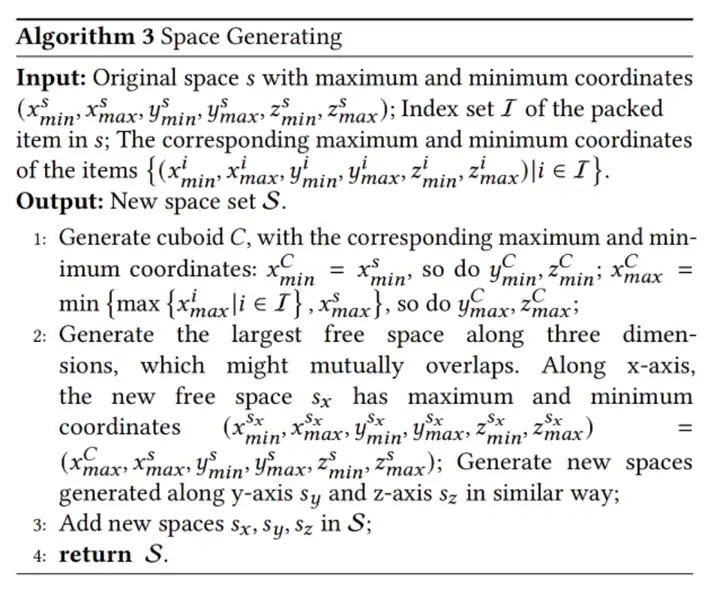
图6是Space generating模块的伪代码,输入是容器s在3个维度上的最小最大坐标(6项内容),容器s中已经放置的物体集合I以及它们在3个维度上的最小最大坐标。由于切分出来的空间通常是要求长方体,因此后续的核心逻辑在于结合前面容器s的坐标以及已放置物体的坐标找出规整的空间,寻找空间的方案比较多,这篇文章采用了最大剩余空间策略。最终,这个模块会输出切分出来的新空间;
3.3 树搜索算法 Tree search algorithm
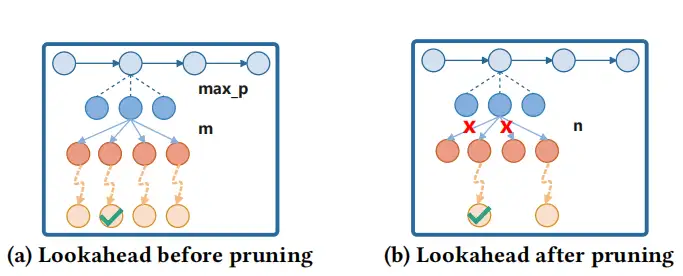
通过前面2个模块可以得到需要放置的新物体-Block集合以及可放置的候选空间-Space集合,接下来的核心问题是如何将Block集合放置到Space集合中。这个问题的解决思路有多种,例如贪心、纯树搜索等。贪心的优点是通常比较快,缺点是具体的效果跟策略本身非常相关,精心设计的贪心策略可能会比搜索类算法要好,但当问题规模比较大时,设计出效果较好的贪心策略并不容易。此外,纯树搜索类算法在小规模问题上确实效果比较好,但是当问题规模逐渐增大时,这类算法的求解效率会降低很多。如图7所示,为了能构造1个效果好且效率也较高的搜索方案,这篇文章提出了一种结合机器学习模型的树搜索算法,其中,机器学习模型的作用是评估以及筛选出得分top-k的搜索分支,主要起到了剪枝的作用。总的来说,图7所示的Greedy LookHead是贪心+机器学习+树搜索的1种组合方案,通过结合不同方案的优点从而实现求解效果以及求解效率的均衡。

虽然在树搜索中,我们应用了 lookahead 过程来加快搜索效率,但 lookahead 过程中需要频繁的调用仿真来模拟装箱过程,仍然会耗费大量的计算时间。因此本论文通过训练一个基于卷积神经网络(CNN)的剪枝模型,减少树搜索中的分支来加速搜索过程,如图所示。
值得一提的是,本文并非直接对候选的block和space pair进行编码建模,而是对于组合容器和装载物体后的整体容器空间进行编码建模,这种建模方式,充分利用了CNN在处理图像上的优异表现,更有效地提取容器和装载货物的空间特征。
State Representation
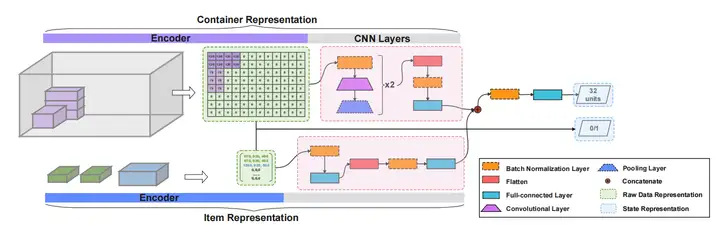
容器装载状态的模型构建如下图,分别通过两种不同的编码和CNN网络提取容器和装载货物的空间特征,其中容器的编码用了一种称为"height map"的方法。"height map"是一个大小为L×W的矩阵,表示容器中每个单元格堆叠物品的高度。物体的编码则包括了物品的长度、宽度和高度,两种编码分别通过图中所示的CNN模型提取特征后再拼接起来,经过正则化后,输出一个32位的张量表示当前装载状态,并额外生成一个0-1布尔值表示容器当前是否为空。
Prune Network
剪枝网络的结构如下图所示,输入是m个由state presentation模型输出的装载状态,首先,将这些状态的特征向量拼接起来,并对其进行归一化处理。然后,应用一个具有Sigmoid激活函数的全连接层,得到一个m维的张量。张量中每个维度的值表示对应位置的状态的分数,接下来,将m个掩码(mask)与m维张量相乘,避免空的装载方案被选中(因为输入层m的维度是固定的,当可行的方案不足m个时,会填充一些空的装载方案补足m个),最终输出层得到每个方案在0-1之间的得分。

Workflow
剪枝模型整体的实现是通过监督学习的方式。首先,我们收集历史订单的分支决策记录。对于每次前瞻过程,我们会前瞻m个装载状态 ,在每个决策的分支上,我们构建分支张量(x, y)。特征x记录了一系列 个状态 的信息,其中 是之前state representation的模型中处理得到的装载状态。特征y是一个长度为 的布尔向量,其中 只有在前瞻到的方案足够多以至被选择时才为1,否则为0。在完成所有历史订单的搜索后,将积累的大量的实例分为训练集和测试集,然后以监督学习的方式学习并保存剪枝网络。通过训练好的网络,我们不需要对前瞻过程中的所有 个分支计算装载率,而是根据剪枝网络的输出只探索前 个有希望的分支。简而言之整个模型通过从历史分支选择过程中学习,以提高未来分支选择的效率。
4 实验分析
4.1 Experimental setup
通过跟四种经典算法(随机算法,构造启发式算法,贪心算法和beam search)比较三个指标(装载率,计算时长,是否实现最优装载)来评估DDTS算法的性能表现。
数据集与参数
评估实验在Linux服务器(操作系统Ubuntu 18.04.4 LTS)上进行,配备 4 个 Intel(R) Xeon(R) Platinum 8180M CPU @ 2.50GHz 和1T内存。树搜索算法主要用Java编写,神经网络模型使用TensorFlow实现。
评估数据集来源于现实世界中华为物流2020年9月至12月的大规模装箱订单数据,总共包含了 1784 个订单,每个订单有 500 到 1000 件商品。所有订单中,平均商品类别数量为61,平均物品数量为 658,平均仓库数量为 5。商品类别总数为 4697 个,总仓库数为71。车辆长宽高分别为 4.1 米、2.3 米和 2.27 米。数据集被随机划分为训练集和测试集,比例为1249 : 535。我们对训练集中所有的订单使用没有剪枝策略的树搜索,共提取25419条分支决策记录,然后使用这些样本来训练和测试剪枝策略网络。
4.2 结果
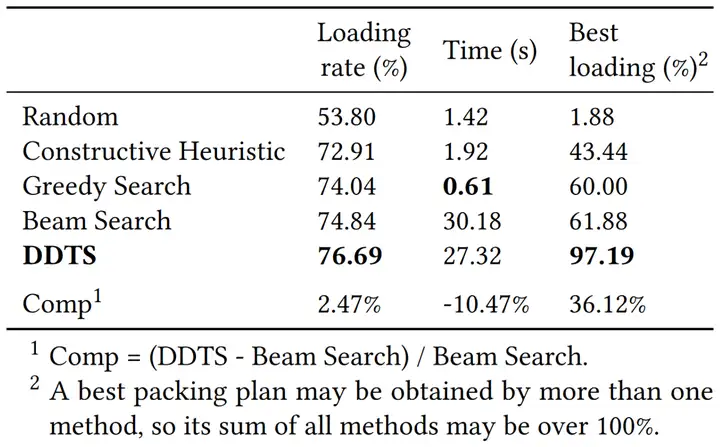
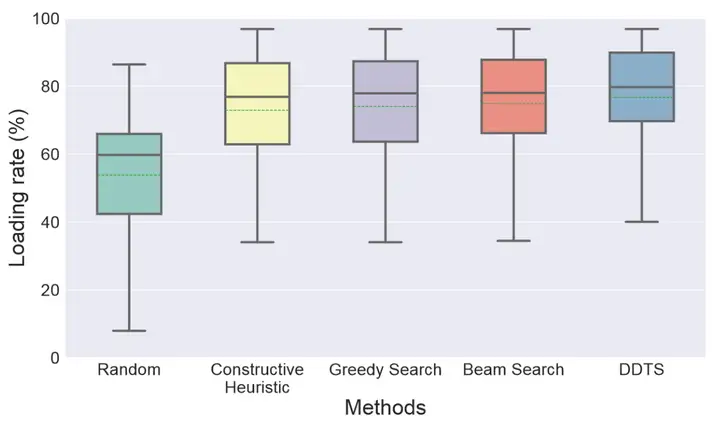
训练出来的剪枝模型在测试集上的准确率为0.89,这说明该模型已经具备了较好的决策能力。更详细的实验指标在表1中呈现,其中“Comp”代表本文算法和最先进算法的比较,即(DDTS - 波束搜索)/ 波束搜索。从表1可知,随机算法的装载率非常低,这表明它还有较大的提升空间。换句话说,尽管问题本身自带了很多约束条件,但不同方法获得的解的质量可能会有较大的差异。启发式类算法的装载率比贪心算法(使用模拟装载过程选择动作)低1%以上,这说明适当选择模拟装载过程的重要性。本文新提出的DDTS在更短时间内获得了76.69%的装载率,比现有算法高2.47%。此外,本文提出的DDTS方法针对所有订单上获得了装载率为97.19%的最佳装箱方案,这说明DDTS在各种订单上都稳定,而不仅仅是在部分订单上表现出色以获得更高的平均装载率,这对实际落地至关重要。图11显示的箱形图说明DDTS的中位装载率和平均装载率均高于其他算法,并且分布更加集中。
4.3 消融实验
4.3.1 约束数量是否影响算法?
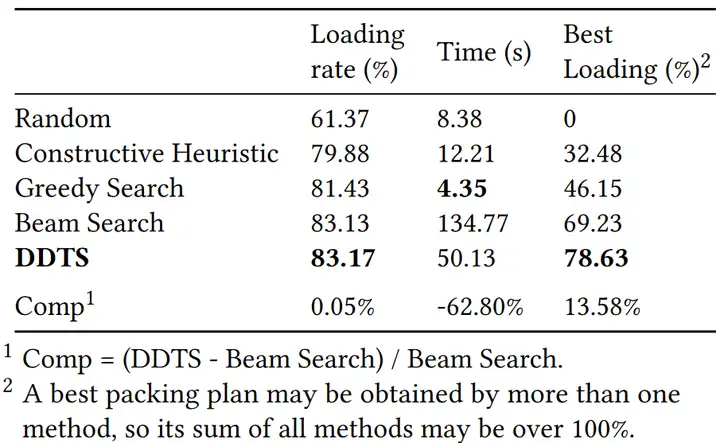
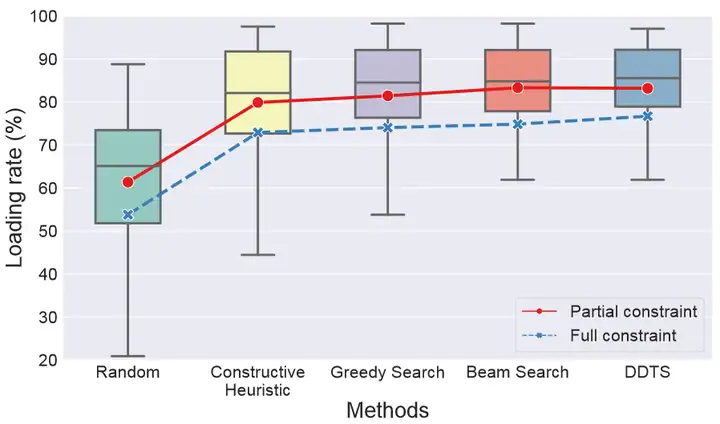
大规模约束是实际场景中最重要的挑战之一,本文在这里研究了约束数量对DDTS的影响。如表2所示,我们通过忽略装载物料约束,方向约束,重量约束等,将约束的数量降低到20。与表1中完整约束版本的结果相比,所有方法的装载率都提高了约7%。在完整约束版本中,Beam Search接近于贪婪搜索,但远远不及DDTS。然而,在部分约束版本中,Beam Search接近于DDTS,远高于贪婪搜索。这说明随着约束规模的增加,Beam Search的性能迅速下降,而DDTS仍然表现极好。此外,通过图12还可以分析部分约束版本所有订单的装载率分布。
4.3.2 物品数量是否影响算法?
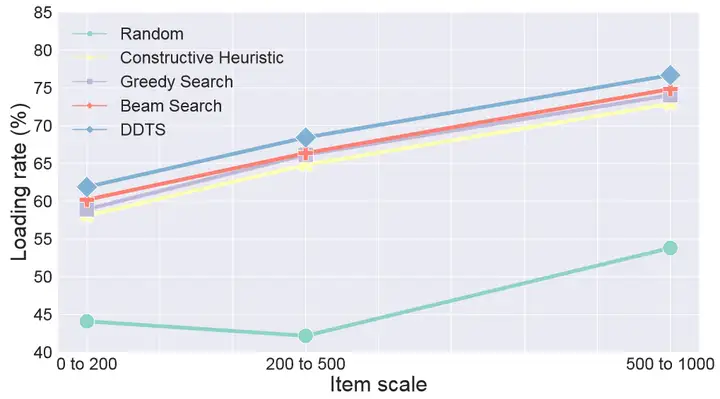
前面的实验都是针对大规模订单,在本节中,通过引入小规模以及中等规模订单来探索待装载物品数量对算法的影响。小规模数据集的订单通常包含0到200个物品,而中等规模数据集的订单则会涉及200到500个物品。所有方法的装载率结果如图13所示,除了随机装载外,其余算法在三个数据集上的表现几乎具有相同的趋势,也就是说,本文提出的DDTS方案在不同物品规模上具有良好的泛化能力。
5 主要结论
该研究针对华为在物流实际应用中的3D-BPP提出了一种基于数据驱动的树形搜索算法(DDTS)来解决传统树搜索算法(TS)耗时长、效率低的问题。在处理大批量的货物时,用到区块组装和空间生成算法,以及在决策时使用lookahead 树搜索算法。除此之外,将基于传统树搜索算法的历史决策行为训练的CNN剪枝网络嵌入到树搜索中以指导修剪,这其实就是类似于运用"专家的历史经验"来减少一些不必要的工作 。
在真实数据集上的实验表明,DDTS的性能优于最先进的方法,货物装载率提高了2.47%。此外,使用剪枝网络加速可以节省37.14%的耗时时长,而性能损失仅为0.04%。DDTS在华为物流系统中部署后,订单平均装载率提高了3%,节省了大量成本。
参考文献
Qianwen Zhu, Xihan Li, Zihan Zhang, Zhixing Luo, Xialiang Tong, Mingxuan Yuan, and Jia Zeng. 2021. Learning to Pack: A Data-Driven Tree Search Algorithm for Large-Scale 3D Bin Packing Problem. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management (CIKM '21). Association for Computing Machinery, New York, NY, USA, 4393–4402. https://doi.org/10.1145/3459637
文章引自https://zhuanlan.zhihu.com/p/654096014




 当前位置:
当前位置:

