本文介绍的是浙江大学光电科学与工程学院刘智毅研究员课题组关于生物组织纤维状结构的组织特征和形态特征定量表征方法的综述,发表在《Journal of Innovative Optical Health Sciences》期刊2023年第4期。
Quantification methodologies on organization and morphology features of fiber-like structures: A review
纤维状结构的组织和形态特征的定量表征方法综述
Chuncheng Wang, Jia Meng, Shuhao Qian, Lingxi Zhou, Shenyi Jiang, Rushan Jiang, Hantao Zhan, Xinguo Fang, Yijie Liu, Zhihua Ding, and Zhiyi Liu*
研究背景
纤维状结构是生物体内最常见的组织结构之一,小到细胞外基质中起支撑作用的胶原纤维、细胞内起物质运输作用的微管,大到输送血液的动脉和静脉血管,纤维状结构在诸多基本生命活动中发挥着重要作用。进而,纤维结构的改变可以反映生物体生理和病理活动的信息,这在生命科学研究和临床应用中具有深刻意义。因此,对纤维状结构细微变化的快速、高精度定量表征,在研究生物组织的结构-功能关系、疾病进展和癌症分期等课题时具有巨大的应用潜力。
内容简介
随着成像方法和计算机技术的发展,表征参量的定义和定量表征算法的建立经历了从人工到全自动方法、从低精度到高灵敏、从二维到三维的过程,从而提高了对成像结果中所蕴含生物信息的提取效率和准确性。本文介绍了一系列定量表征参量及其计算方法,用以描述生物组织纤维状结构的组织和形态特征:从空间取向开始,其与生物组织功能、基因表达和病理变化高度相关;然后介绍与纤维取向分布密切相关的弯曲度;最后讨论粗细度特征。这些表征参量和方法为生命科学研究提供了强有力的工具,对临床诊疗具有重要意义。
图文导读
1. 纤维状结构空间取向的定义

图1:描述空间取向角度的定义。 (a) 在二维空间用方位角θ表示空间取向。 (b) 在三维空间中用方位角θ和极角φ表示空间取向。
纤维状结构在二维平面中的空间取向由方位角θ(0°到180°)精确描述,θ被定义为平面内纤维(蓝线)与x轴之间的角度,如图1a所示。在三维空间中,纤维(蓝线)的空间取向由方位角θ和极角φ共同描述,θ定义为纤维在xy平面上的投影与x轴之间的夹角,极角φ定义为纤维与极轴之间的夹角,在本例中极轴为-z轴,如图1b所示。类似地,θ和φ都在0°和180°之间的范围内。由此可以描述在空间中具有任意取向的纤维状结构。
2.用于表征纤维状结构空间取向的傅里叶变换方法和权重矢量求和算法
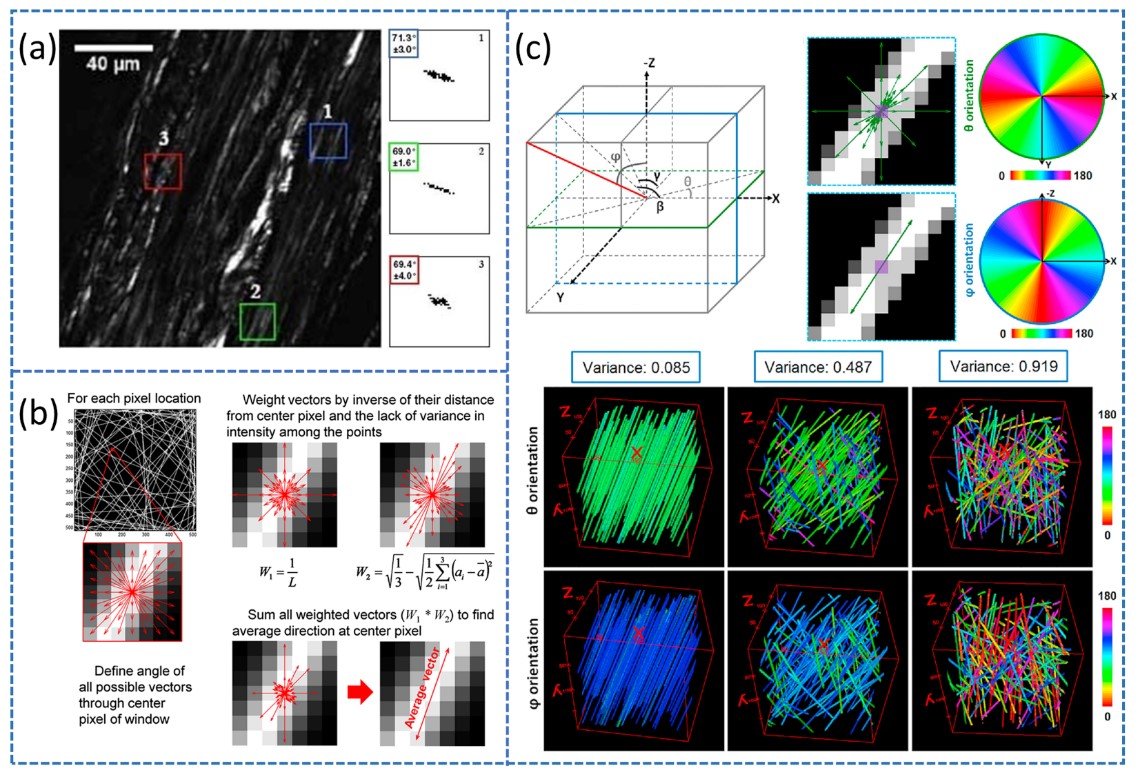
图2:用于表征纤维状结构空间取向的两种方法的示意图。 (a) 胶原纤维二次谐波产生图像的傅里叶变换结果。 (b) 二维矢量加权求和算法示意图。 (c) 三维矢量加权求和算法和衍生的表征空间有序度的三维方向方差仿真示意图。
早期常用傅立叶变换二次谐波生成(FT-SHG)的成像和定量分析方法,表征胶原纤维的空间取向特征:通过对感兴趣区域进行二维傅立叶变换,对应频谱中高强度频率的取向通常为垂直于大多数胶原纤维排列的取向;进一步对傅里叶变换频谱进行二值化,可以使主空间频率突出,如图2a所示。二维的矢量加权求和算法极大地提高了表征精度:通过对窗口内所有穿过中心像素的可能的对称矢量,赋予长度和强度涨落有关的两项权重因子,将所有加权向量求和即可获得中心像素的空间方向,如图2b所示。三维空间中方位角θ的计算与二维平面类似,而极角φ可通过与方位角θ相似的两个额外的角度转化而来。进一步提出了用于定量表征纤维状结构空间有序度的参量:三维方向方差,当纤维相互平行时,参量值接近0;而当纤维随机分布时,方差值更接近1,相应的仿真结果如图2c所示。
3.基于扩散张量核磁共振成像技术的空间取向计算方法
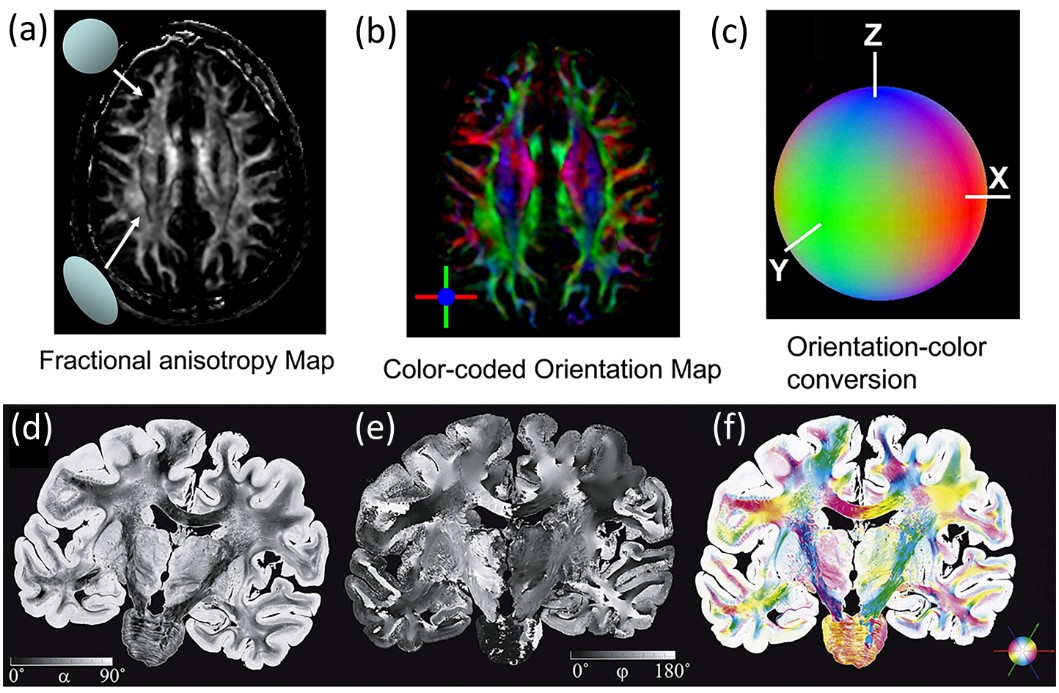
图3:扩散张量核磁共振成像技术和3D偏振光成像定量表征方法。(a)大脑纤维束的部分各向异性图谱。(b)彩色编码的大脑纤维束三维取向图谱。(c)图(b)的三维方向对应的颜色转换图例。(d)大脑切片的极角分布灰度编码图谱。(e)大脑切片的方位角分布灰度编码图谱。(f)集成了极角和方向角分布信息的HSV颜色编码方向图。
基于水分子自扩散特性的扩散张量磁共振成像(DT-MRI)或扩散张量成像(DTI)技术,能够提升医学影像空间分辨率和对比度。根据成像结果可以定义“分数各向异性”(FA)来表征扩散各向异性,表示纤维排列程度范围,其值分布区间为从0(各向同性)到1(各向异性)。分级结果可以通过灰度编码 (图3a) 或彩色编码 (图3b,c) 进行可视化。基于轴突外髓鞘的固有双折射特性,三维偏振光成像(3D-PLI)同样可以用来对人脑神经纤维束的空间取向进行定量成像。定量表征的极角图 (图3d) 和方位角图 (图3e) 既可以通过灰度编码实现可视化,又可以组合生成假彩色编码的三维取向图 (3D-FOM,图3f)。
4. 空间取向定量表征算法的应用

图4:空间取向的不同定量表征方法的应用示例。 (a) 从傅里叶变换-二次谐波方法获得的原始图像和表征结果。 (b) 轴突、丝纤维、胶原和MCF10A细胞培养物的原始图像和通过二维矢量求和算法获得二维取向图。 (c) 三维加权求和算法和方向方差算法应用于对小鼠关节软骨不同层的建模和区分。 (d) 心肌梗死发生后不同时间点心脏组织胶原纤维和交联的定量表征图像。
图4a展示了使用二维和三维傅里叶变换方法对网格化的二次谐波图像进行分析,生成了背景、各向同性和取向标记的三元标签图,以评估小鼠子宫颈胶原纤维组织的空间取向。而二维矢量加权求和算法在定量表征多种纤维状组织结构的空间取向时,依然能够保持像素级的精度,如图4b所示。进一步地,三维矢量加权求和算法和三维方向方差参数对小鼠关节软骨物理结构的建模,体现出了其在识别三维空间结构特点方面的优越性,如图4c所示。此外,由于交联结构对特定激发波长的双光子荧光显微信号敏感,成像结果的信号强度可以直接反映生物组织中交联水平;如图4d所示,相关分析结果表明,交联水平的增加,与小鼠从心肌梗死中恢复时胶原纤维排列的取向呈现关联。
5. 纤维状结构弯曲程度的表征方法
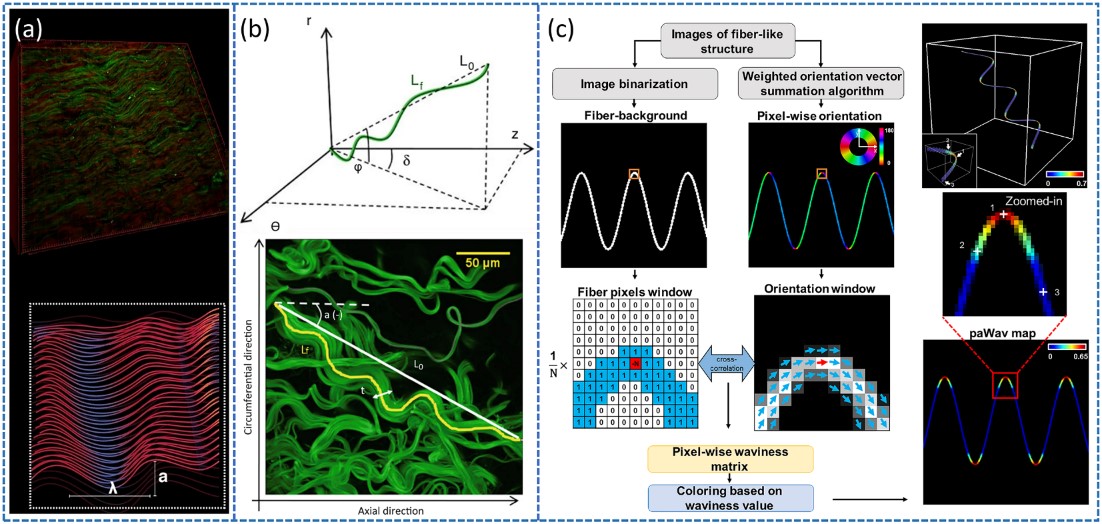
图5:弯曲程度定量表征方法示意图。 (a) 人体声带弹性蛋白和胶原纤维的三维重构及准正弦波状线形描述示意图。 (b)三维和二维空间直线度参数定义的示意图。 (c) 表征弯曲度的paWav参数计算流程和仿真结果。
从图5a双光子荧光显微图像和二次谐波图像的三维重构中可以看到,声带中的弹性蛋白(红色)和胶原纤维(绿色)呈现出准正弦信号的图样,可以近似地用具有振幅值a和空间周期值λ的正弦信号描述,二者之比即长宽比也可以近似地作为量化弯曲程度的指标。不规则弯曲结构的定义较为困难,可以用“直线度”参数(Ps)来粗略估计,即纤维两端之间的直线距离与纤维实际长度的比值,完全直的纤维接近1,弯曲程度高的纤维接近0,如图5b所示。另有一种在像素/体素精度上自动提取纤维状结构弯曲度(paWav)的算法,如图5c所示,算法基于空间取向定量表征结果的矩阵,将某像素周围一定范围内的纤维的空间取向值与该像素的空间取向值作差,取绝对值后进行归一化,即可得到纤维在该像素处的paWav参量。
6. 弯曲程度定量表征方法的应用
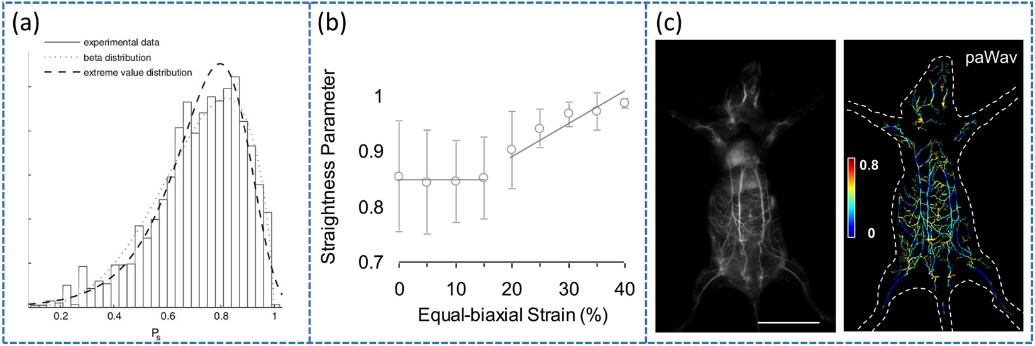
图6:不同弯曲程度定量表征算法的分析结果。(a)β分布和极值分布对兔颈动脉外膜胶原纤维的直线度参数直方图分布拟合。(b)猪胸主动脉外膜胶原纤维平直度对等双轴应力响应。(c)小鼠全身血管的原始图像和paWav彩色编码分布图。
定量表征纤维状结构结果的呈现形式有很多。图6a展示了NeuronJ所提取的兔颈动脉外膜胶原纤维直线度的概率分布,并发现β分布对零应力下胶原纤维平直度概率分布的拟合程度比极值分布表现更好。图6b为NeuronJ应用于定量表征猪胸主动脉外膜弹性蛋白和胶原纤维在加载机械应力过程中的平直度变化,结果表明高于20%的应力会显著增加胶原纤维的平直度。图6c介绍了小鼠全身血管的原始图像及彩色编码的paWav参量像素级分布图谱,显示出该方法能对大尺度血管的弯曲程度实现像素级高精度的定量表征,且输出的彩色编码图谱具有很好的直观性。
7. 血管粗细度定量表征方法
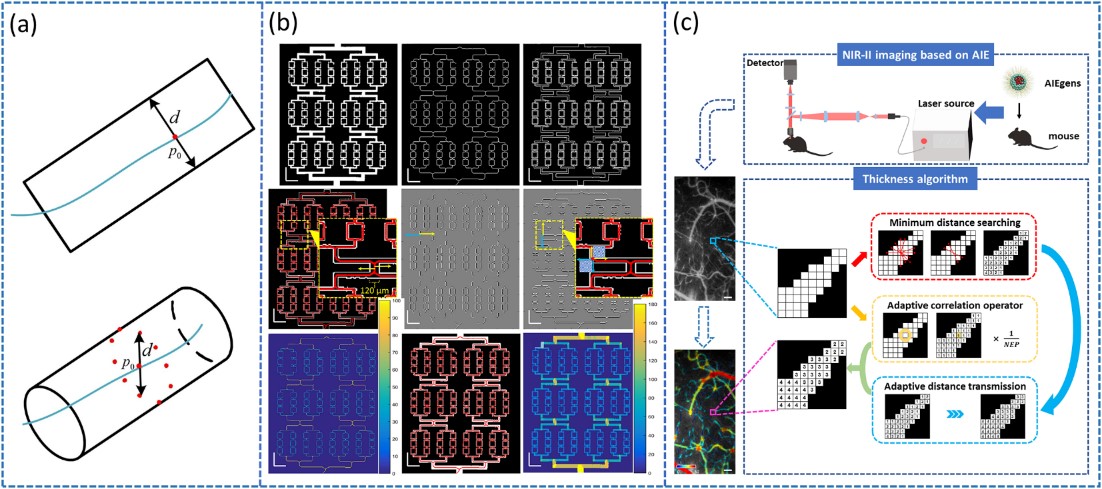
图7:血管粗细度定量表征方法示意图。(a)二维和三维边界相交方法示意图。(b)梯度引导最小径向距离算法实现粗细度定量表征。(c)基于自适应窗口的血管粗细度量化算法示意图。
血管是一种在粗细度上跨度较大的纤维状结构。在二维图像中,通常采用计算血管两个边缘之间距离来实现对血管粗细度的量化,如图7a上半部分所示;而在三维空间中,血管为圆柱形结构,需要使用三维边界相交的方法来量化血管粗细度,先后经过血管骨架线和边缘提取、迭代圆拟合和平均化实现对血管直径的估计,如图7a下半部分所示。另外一种方法使用梯度引导的最小径向距离算法(MRD)来定量表征血管直径,依次经过图像二值化、生成血管骨架图和血管边缘图、计算骨骼到边缘的最小距离和对两边缘距离值加和来估计血管粗细度,如图7b仿真所示。最近提出的像素级表征方法依次使用二值化、距背景最小距离计算、自适应距离传输和平滑处理,最终以伪彩色编码输出像素级高精度的血管粗细度图谱,如图7c所示。
8. 血管粗细度定量表征方法的应用
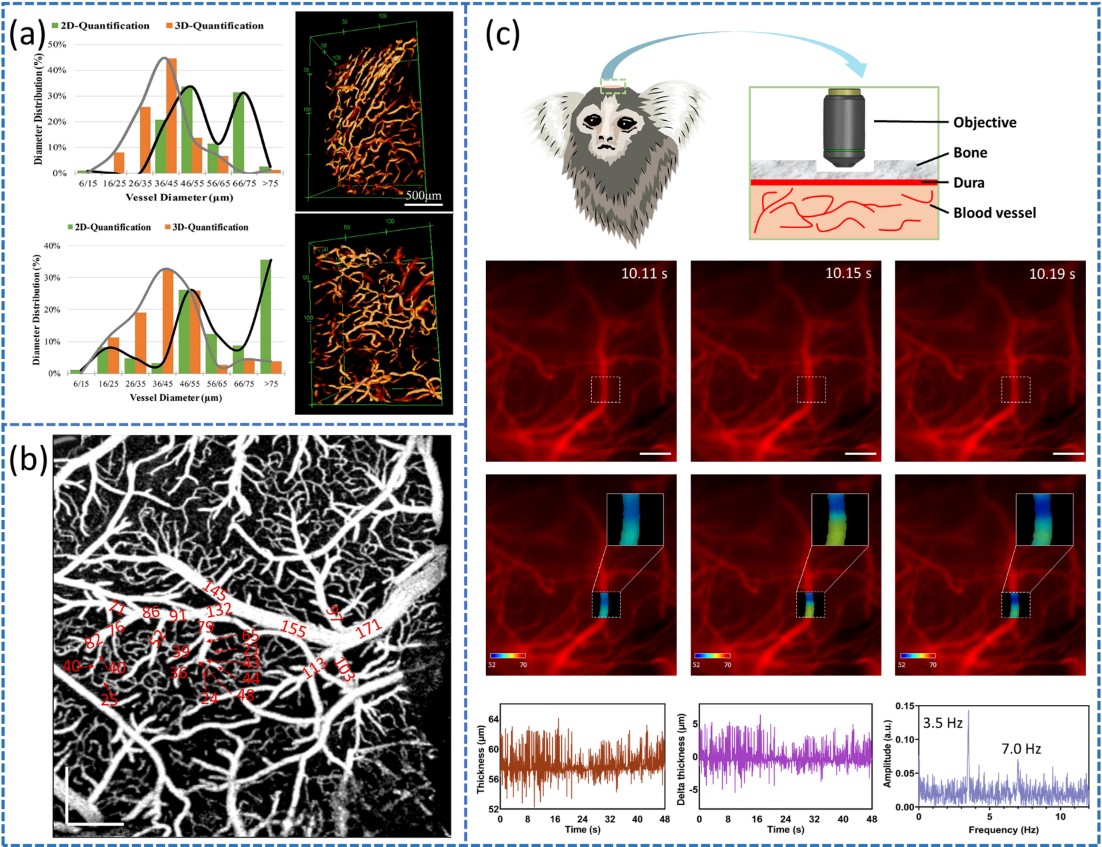
图8:血管粗细度定量方法的应用实例。(a)通过边界相交法提取的血管直径直方图,以及相应的三维渲染图。(b)通过MRD方法结合血管追踪算法标记平均血管粗细度的OCTA血管造影照片。(c)狨猴脑血管粗细度的逐像素动态监测。
在表征光声成像结果中的肿瘤血管粗细度时,表征结果的概率分布显示三维算法能更好地区分直径相似的血管,如图8a所示。在表征光学相干断层扫描血管造影(OCTA)图像中小鼠脑血管系统的粗细度时,使用MRD方法和血管追踪相结合计算、在局部分支做平均粗细值标记的方法,比基于直方图的原位标记方法提供了更详细的结果,如图8b所示。在定量表征三光子荧光显微成像结果中狨猴脑血管的粗细度时,算法以高灵敏度识别了血管粗细度随时间的动态变化,输出的逐像素血管粗细度图谱不仅在可视化和准确性方面表现出色,而且适用于心跳频率等统计分析,如图8c所示。
总的来说,近年来纤维状结构定量表征算法的发展,极大地提高了对生物医学影像中信息的利用率。未来,随着高分辨率/超分辨率显微技术的进步,更多快速、高精度的定量表征方法将在科学研究和临床应用发挥更大的作用。
通讯作者简介

刘智毅,浙江大学光电科学与工程学院“百人计划”研究员,博士生导师。工作围绕先进光学成像方法的构建与图像的定量表征展开,致力于光学图像与疾病的关联性研究。迄今,在Science Advances,Laser & Photonics Reviews等国际期刊发表论文50 余篇。申请和授权了多项中国、美国专利。多次在国际会议上作邀请报告和口头报告。担任了Science Advances等20余本国际主流期刊的审稿人。获第五届全国高等学校电子信息类专业青年教师授课竞赛一等奖。以负责人身份,主持国家重点研发计划项目,国家自然科学基金青年、面上项目,浙江省自然科学基金杰出青年项目等。